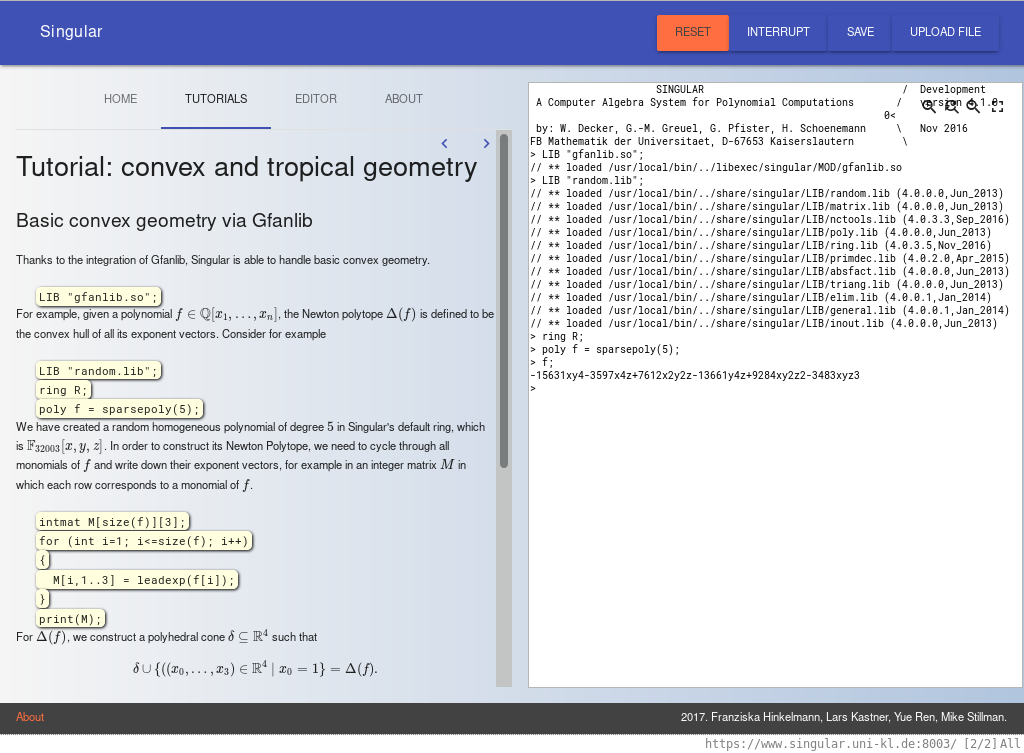
#Current Challenges
in the
#Development
of
#Open Source
#Computer Algebra Software
My name is
#Christian Eder
I'm from the
#University of Kaiserslautern
#DFG Collaborative
#Research Center
#TRR 195
Kaiserslautern, Aachen, Saarbrücken
+ many others
Methods from Computer Algebra
are nowadays firmly established
in the toolbox of the pure
mathematician.
Fruitful interactions between
.
Algebraic Geometry,
Computer Algebra,
Group & Representation Theory,
Number Theory and
Polyhedral Geometry
Our approach
#OSCAR
Open Source
Computer Algebra
Resource
Four
cornerstones
#GAP
group & representation theory,
general purpose high level
interpreted language
*GAP* - Projective Special Linear Groups
.
gap> grp:=PSL(5,3);;
gap> a:=PseudoRandom(grp);;
gap> b:=PseudoRandom(grp);;
.
gap> Size( Group(a,b) );
237783237120 // 10 msec on this machine
#SINGULAR
polynomial computations in
algebraic geometry,
commutative algebra &
singularity theory
*SINGULAR* -
Parametrization of rational curves
.
> LIB"paraplanecurves.lib";
> ring r = 0,(x,y,z),dp;
> poly f = x5+10x4y+20x3y2+130x2y3-20xy4+20y5
. -2x4z-40x3yz-150x2y2z-90xy3z
. -40y4z+x3z2+30x2yz2+110xy2z2+20y3z2;
.
> genus(f); // may require blow-ups
0
> paraPlaneCurve(f); // normalization, integral bases
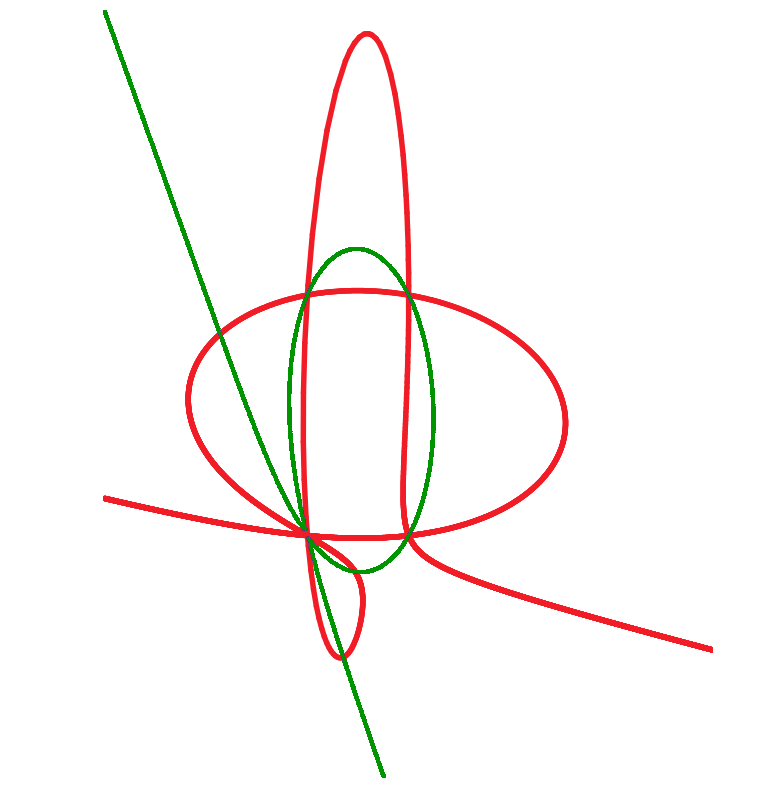 #polymake
convex polytopes, polyhedral fans,
simplicial complexes, related objects
from combinatorics & geometry
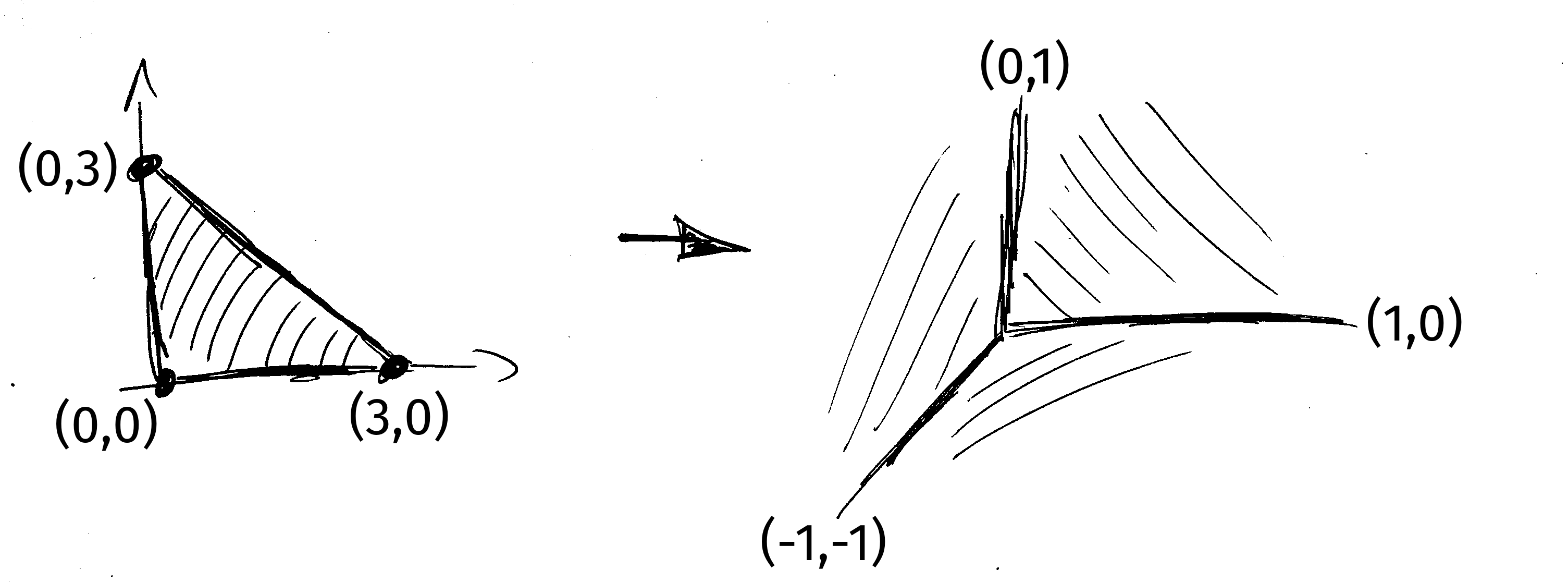
*polymake* - Normal fans (via SINGULAR)
.
> LIB"polymake.so"; // credits for polymake
> ring r=0,(x,y),dp;
> poly f=x3+y3+1; // last SINGULAR-only statement
.
> polytope p = newtonPolytope(f);
> fan F = normalFan(p);
> F;
RAYS: MAXIMAL CONES:
-1 -1 #0 {0 1} #Dimension 2
0 1 #1 {0 2}
1 0 #2 {1 2}
#polymake
convex polytopes, polyhedral fans,
simplicial complexes, related objects
from combinatorics & geometry
*polymake* - Normal fans (via SINGULAR)
.
> LIB"polymake.so"; // credits for polymake
> ring r=0,(x,y),dp;
> poly f=x3+y3+1; // last SINGULAR-only statement
.
> polytope p = newtonPolytope(f);
> fan F = normalFan(p);
> F;
RAYS: MAXIMAL CONES:
-1 -1 #0 {0 1} #Dimension 2
0 1 #1 {0 2}
1 0 #2 {1 2}
 #ANTIC
number theory software, computations
in & with number fields and generic
finitely presented rings
.
created within SPP-1489
*ANTIC* - Class Groups & Extended GCDs
.
> Qx, x = PolynomialRing(QQ, "x")
> f = x^6+141*x^5-141*x^4+141*x^3-141*x^2+141*x-141
> K, a = NumberField(f);
> M = lll(maximal_order(K));
> class_group(M)
.
> Kt, t = PolynomialRing(K, "t")
> g = sum([K(rand(M, 100))*t^i for i=1:20])
> h = sum([K(rand(M, 100))*t^i for i=1:20])
> @time gc, a, b = gcdx(g, h);
#ANTIC
number theory software, computations
in & with number fields and generic
finitely presented rings
.
created within SPP-1489
*ANTIC* - Class Groups & Extended GCDs
.
> Qx, x = PolynomialRing(QQ, "x")
> f = x^6+141*x^5-141*x^4+141*x^3-141*x^2+141*x-141
> K, a = NumberField(f);
> M = lll(maximal_order(K));
> class_group(M)
.
> Kt, t = PolynomialRing(K, "t")
> g = sum([K(rand(M, 100))*t^i for i=1:20])
> h = sum([K(rand(M, 100))*t^i for i=1:20])
> @time gc, a, b = gcdx(g, h);

 Design & development
of a CAS in general
driven by intended
applications
Mathematical
applications
Mumford (1980):
.
Can a computer classify all surfaces of
general type with pg = 0?
Let X be a minimal surface
of general type with pg=0
such that (KX)2 = 1
.
→ numerical *Godeaux surfaces*
X Godeaux surface
.
⇒ H1(X,ℤ) is cyclic of
⇒ order at most 5
.
Constructions have been
given for each such order.
Conjecture:
.
There is precisely one irreducible
family of surfaces for each order.
Experimental approach to
solve this conjecture:
.
1. Construct random points
1. in moduli spaces.
.
2. Study related geometry
2. via CAS.
Requirements for this approach:
.
1. Computational Algebraic Geometry
2. Topology
3. Group Theory
Joint project by
.
Wolfram Decker & Isabel Stenger
(Kaiserslautern)
Frank-Olaf Schreyer
(Saarbrücken)
.
in collaboration with Miles Reid
(Warwick)
Why is this computationally hard
from the very beginning?
.
> Rextension;
// characteristic : 0
// 1 parameter : a
// minpoly :
(24873879473832817299558394474990433025260537858429700*a^8
+412197480758832021377448558823165698794277118212212070*a^7
+625366891611244986389942014312773193649951168354090190*a^6
-436561073546512334083477547357856090524552855592558795*a^5
-914947642504230095779800456657440020138074539186145912*a^4
-2227325279423247966617649640155997715235288113299887954*a^3
+2312070077580715288467637707530192772778088469836344950*a^2
+1366053134215201364075122803745127996518986576734818612*a
-1156759915557562158859054495379551857229358735237021536)
// number of vars : 12
"Non-mathematical"
applications
#High Energy Phsyics
joint work with
Pierpaolo Mastrolia and Tiziano Peraro
Design & development
of a CAS in general
driven by intended
applications
Mathematical
applications
Mumford (1980):
.
Can a computer classify all surfaces of
general type with pg = 0?
Let X be a minimal surface
of general type with pg=0
such that (KX)2 = 1
.
→ numerical *Godeaux surfaces*
X Godeaux surface
.
⇒ H1(X,ℤ) is cyclic of
⇒ order at most 5
.
Constructions have been
given for each such order.
Conjecture:
.
There is precisely one irreducible
family of surfaces for each order.
Experimental approach to
solve this conjecture:
.
1. Construct random points
1. in moduli spaces.
.
2. Study related geometry
2. via CAS.
Requirements for this approach:
.
1. Computational Algebraic Geometry
2. Topology
3. Group Theory
Joint project by
.
Wolfram Decker & Isabel Stenger
(Kaiserslautern)
Frank-Olaf Schreyer
(Saarbrücken)
.
in collaboration with Miles Reid
(Warwick)
Why is this computationally hard
from the very beginning?
.
> Rextension;
// characteristic : 0
// 1 parameter : a
// minpoly :
(24873879473832817299558394474990433025260537858429700*a^8
+412197480758832021377448558823165698794277118212212070*a^7
+625366891611244986389942014312773193649951168354090190*a^6
-436561073546512334083477547357856090524552855592558795*a^5
-914947642504230095779800456657440020138074539186145912*a^4
-2227325279423247966617649640155997715235288113299887954*a^3
+2312070077580715288467637707530192772778088469836344950*a^2
+1366053134215201364075122803745127996518986576734818612*a
-1156759915557562158859054495379551857229358735237021536)
// number of vars : 12
"Non-mathematical"
applications
#High Energy Phsyics
joint work with
Pierpaolo Mastrolia and Tiziano Peraro
 For example,
.
> ring r=(0,p11,p12,p22,e34,m1,m2,m3),(x1,x2,x3,x4),dp;
.
> poly D1=2*x3*x4*e34+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-m1;
> poly D2=-m2+2*x3*x4*e34-2*p11*x1+p11+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-2*p12*x2;
> poly D3=2*x3*x4*e34+2*x1*p12-m3+x1*(p11*x1+p12*x2)+p22
. +(x1*p12+p22*x2)*x2+2*p22*x2;
.
> ideal I = D1, D2, D3;
> ideal GI = groebner(I);
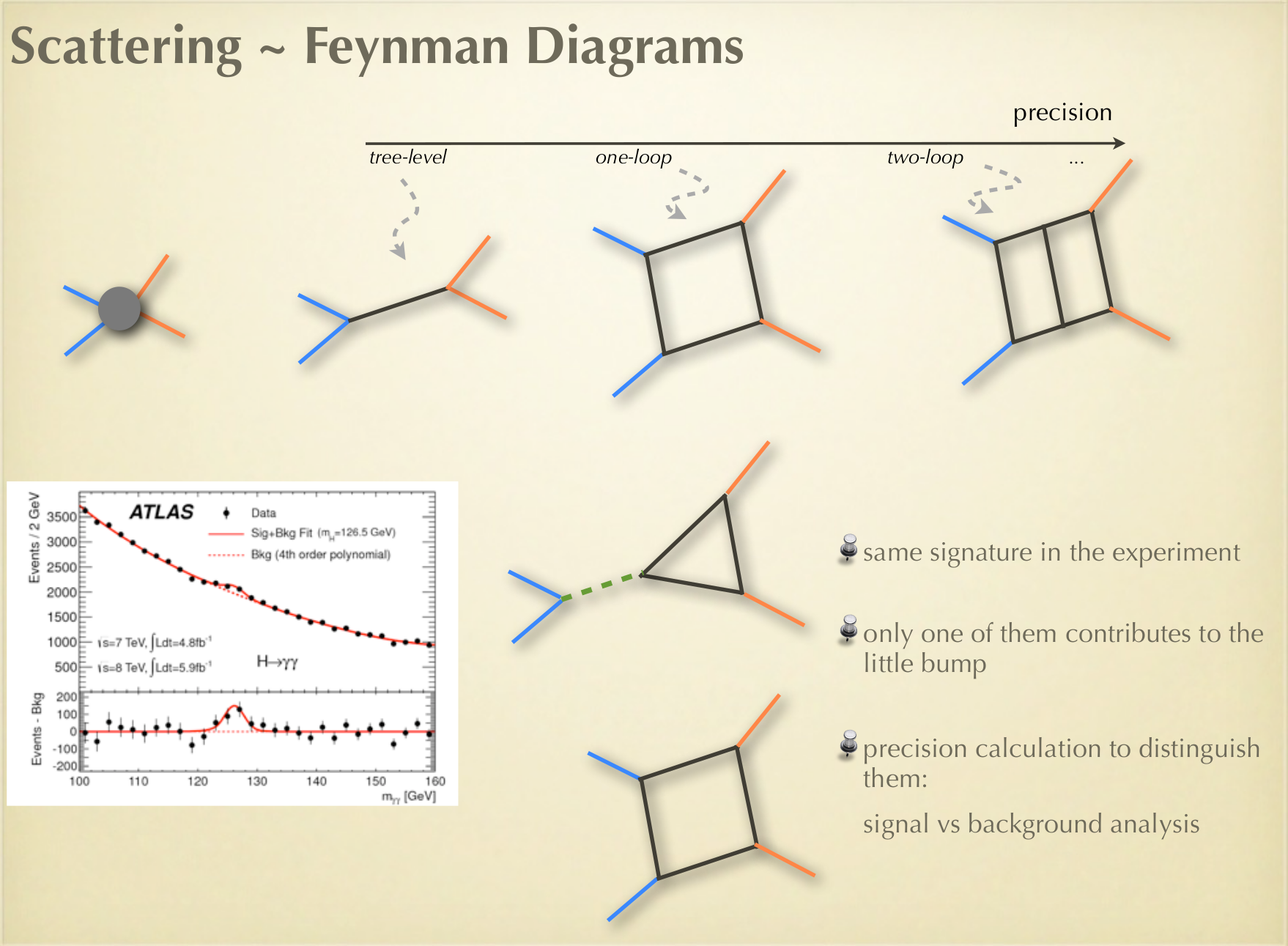
#Challenge #1
Efficiency of Fundamental Algorithms
Low level Implementations
.
*Gröbner Bases* & *Standard Bases*
*Syzygies* & *Free Resolutions*
*Polynomial Factorization*
*F4 Algorithm* for SINGULAR
.
based on special-purpose
linear algebra library *GBLA*
.
joint work with
Jean-Charles Faugère
& the PolSys team
For example,
.
> ring r=(0,p11,p12,p22,e34,m1,m2,m3),(x1,x2,x3,x4),dp;
.
> poly D1=2*x3*x4*e34+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-m1;
> poly D2=-m2+2*x3*x4*e34-2*p11*x1+p11+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-2*p12*x2;
> poly D3=2*x3*x4*e34+2*x1*p12-m3+x1*(p11*x1+p12*x2)+p22
. +(x1*p12+p22*x2)*x2+2*p22*x2;
.
> ideal I = D1, D2, D3;
> ideal GI = groebner(I);
#Challenge #1
Efficiency of Fundamental Algorithms
Low level Implementations
.
*Gröbner Bases* & *Standard Bases*
*Syzygies* & *Free Resolutions*
*Polynomial Factorization*
*F4 Algorithm* for SINGULAR
.
based on special-purpose
linear algebra library *GBLA*
.
joint work with
Jean-Charles Faugère
& the PolSys team



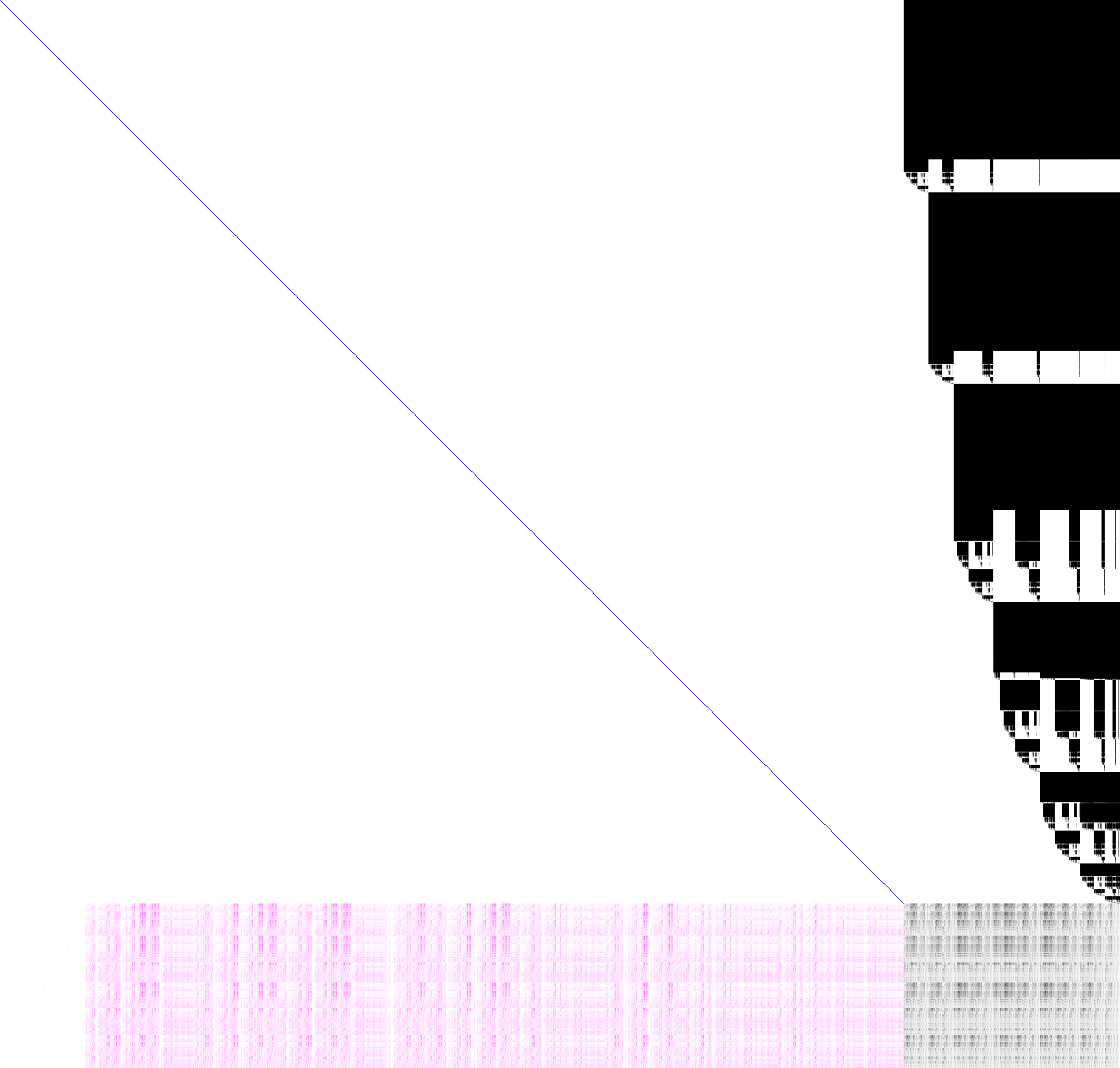
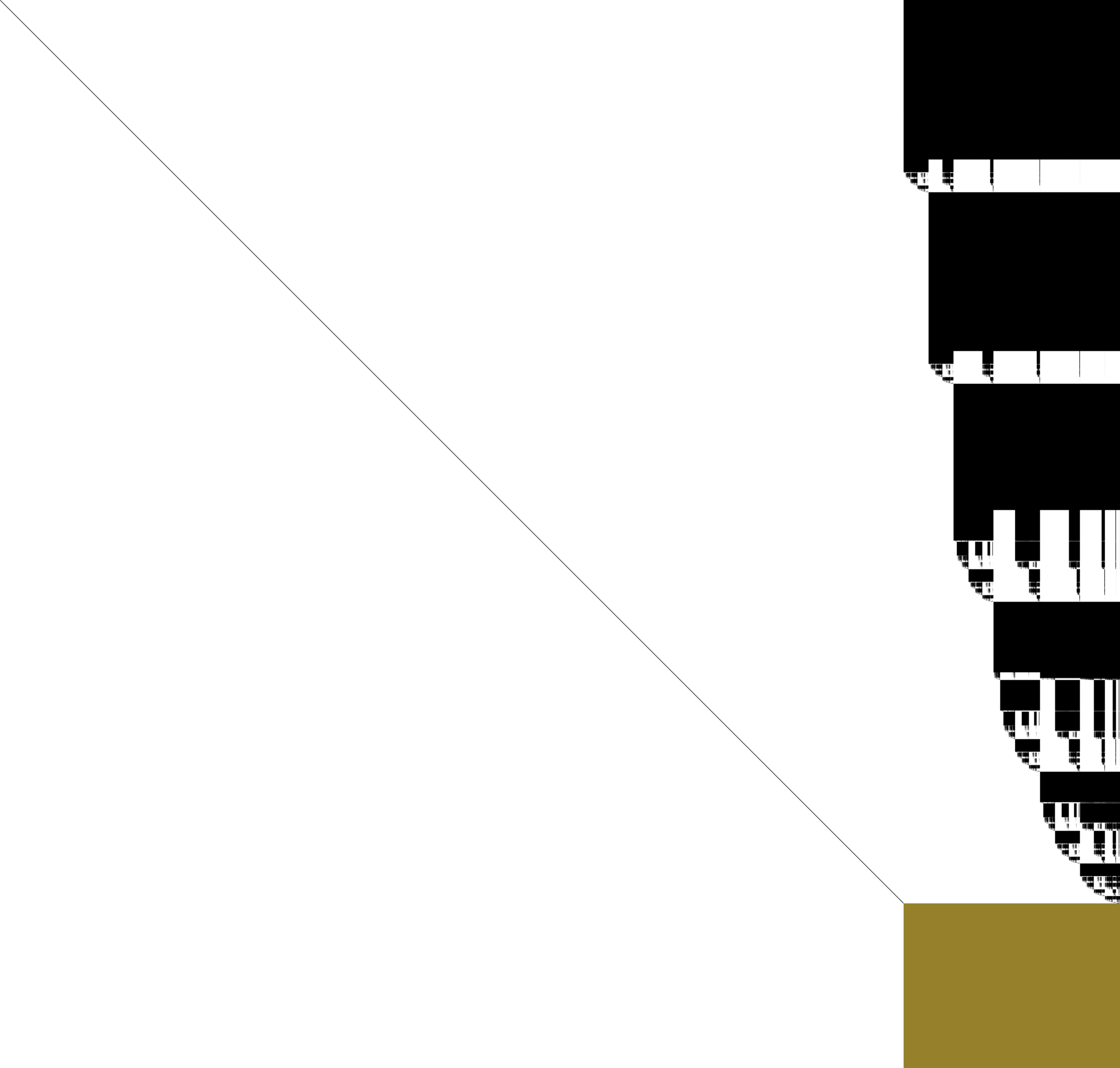
 High level Implementations
*Primary decomposition*
(Gianni-Trager-Zacharias,
Shimoyama-Yokoyama,
Eisenbud-Huneke-Vasconcelos)
.
*Normalization*
(de Jong, Greuel-Laplagne-Seelisch)
.
analyzing *Singularities*
(Hamburger-Noether expansions, blow-ups,
resolution of singularities, etc.)
Other Packages
High level Implementations
*Primary decomposition*
(Gianni-Trager-Zacharias,
Shimoyama-Yokoyama,
Eisenbud-Huneke-Vasconcelos)
.
*Normalization*
(de Jong, Greuel-Laplagne-Seelisch)
.
analyzing *Singularities*
(Hamburger-Noether expansions, blow-ups,
resolution of singularities, etc.)
Other Packages
 *CHEVIE*
Symbolic calculations with generic
character tables of groups
of Lie type & more
(Geck-Hiß-Lübeck-Malle-Michel-Pfeiffer)
*homalg*
Constructive homological algebra
(Barakat-Gutsche-Lange-Hegemann-Posur)
.
*CAP*
Category theory part for homalg
(Gutsche-Posur)
*FLINT*
Fast library for number theory
(Hart-Johansson-et al)
*NEMO*
Algebraic number theory,
recursive generic rings
(Fieker-Hart-Hofmann-Johansson-Motsak)
*HECKE*
Class groups, orders in number fields,
lattice enumeration, sparse linear algebra
(Fieker-Hofmann)
*A-TINT*
Algorithmic tropical
intersection theory
(Hampe)
even more packages
.
*4ti2*
*cddlib*
*Gfan*
*normaliz*
& many more
Challenge #2
Parallelization
Thread Level
(fine grain)
*CHEVIE*
Symbolic calculations with generic
character tables of groups
of Lie type & more
(Geck-Hiß-Lübeck-Malle-Michel-Pfeiffer)
*homalg*
Constructive homological algebra
(Barakat-Gutsche-Lange-Hegemann-Posur)
.
*CAP*
Category theory part for homalg
(Gutsche-Posur)
*FLINT*
Fast library for number theory
(Hart-Johansson-et al)
*NEMO*
Algebraic number theory,
recursive generic rings
(Fieker-Hart-Hofmann-Johansson-Motsak)
*HECKE*
Class groups, orders in number fields,
lattice enumeration, sparse linear algebra
(Fieker-Hofmann)
*A-TINT*
Algorithmic tropical
intersection theory
(Hampe)
even more packages
.
*4ti2*
*cddlib*
*Gfan*
*normaliz*
& many more
Challenge #2
Parallelization
Thread Level
(fine grain)


 *Problem*
Many fundamental algorithms
are sequential in nature
Process Level
(coarse grain)
General scheme for
*modular methods*
for algorithms
over the rationals.
e.g. GBs over the rationals
(Arnold, Idrees-Pfister-Steidel,
(& many more)
or GBs over algebraic number fields
(Boku-Decker-Fieker-Steenpaß)
*Problem*
Many fundamental algorithms
are sequential in nature
Process Level
(coarse grain)
General scheme for
*modular methods*
for algorithms
over the rationals.
e.g. GBs over the rationals
(Arnold, Idrees-Pfister-Steidel,
(& many more)
or GBs over algebraic number fields
(Boku-Decker-Fieker-Steenpaß)
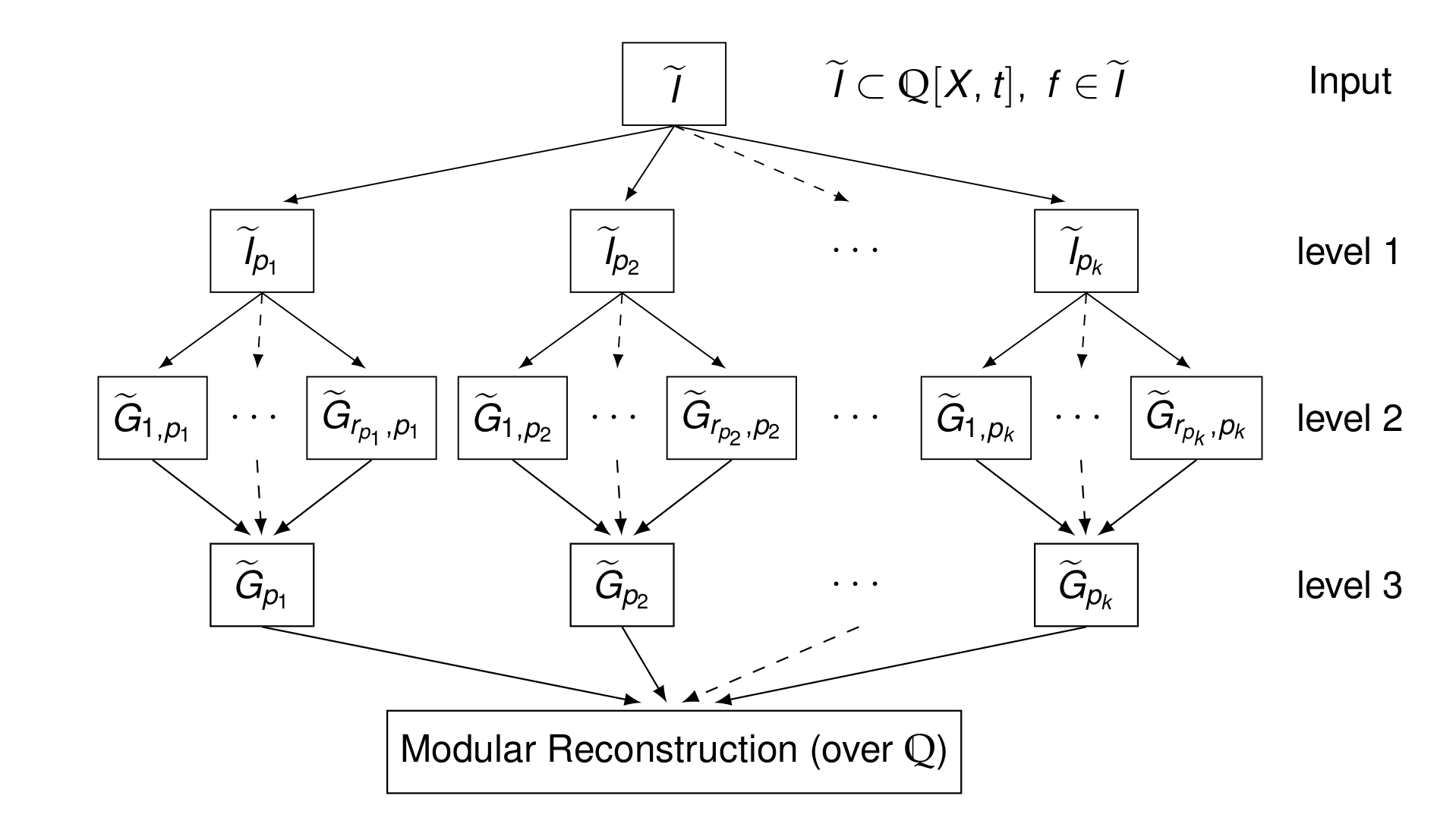 Or try to find new approaches
*Local-to-global Approach* to Normalization
(Böhm-Decker-Laplagne-Pfister-Steenpaß-Steidel)
.
1. Stratify the singular locus.
2. Compute local contribution to the
2. normalization at each stratum.
3. Put the local contributions back together.
How to combine different
levels of parallelization
in a *convenient* way?
.
Experts? Non-experts?
*Btw:*
x86 CPUs are not the
whole picture
Or try to find new approaches
*Local-to-global Approach* to Normalization
(Böhm-Decker-Laplagne-Pfister-Steenpaß-Steidel)
.
1. Stratify the singular locus.
2. Compute local contribution to the
2. normalization at each stratum.
3. Put the local contributions back together.
How to combine different
levels of parallelization
in a *convenient* way?
.
Experts? Non-experts?
*Btw:*
x86 CPUs are not the
whole picture
 #Cluster of 256 Raspberry Pis
(src: https://www.raspberrypi.org/magpi/seemore/)
massively-parallel multicore processors,
on-chip / discrete GPUs, ARM chips,
heterogenous computation (OpenCL),
distributed computation on our
phones & tablets, ...
#Challenge #3
Make Abstract Concepts of Pure
Mathematicians Constructive
*Category Theory*
influenced object-oriented
& functional programming
#Cluster of 256 Raspberry Pis
(src: https://www.raspberrypi.org/magpi/seemore/)
massively-parallel multicore processors,
on-chip / discrete GPUs, ARM chips,
heterogenous computation (OpenCL),
distributed computation on our
phones & tablets, ...
#Challenge #3
Make Abstract Concepts of Pure
Mathematicians Constructive
*Category Theory*
influenced object-oriented
& functional programming
 #Wormholes in mathematics
#Wormholes in mathematics
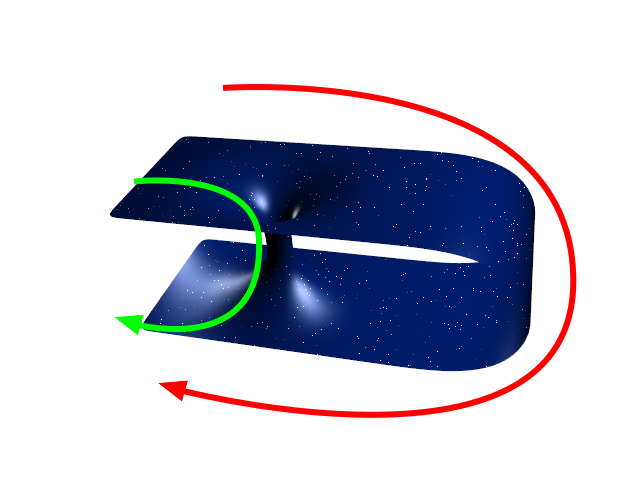 (license: GNU-FDL, made by Panzi)
1. Translate problems in entirely different context.
2. Switch to more efficient data structures.
3. Get reduced computational complexity.
#Challenge #4
A Convenient Hierarchy of Languages
(license: GNU-FDL, made by Panzi)
1. Translate problems in entirely different context.
2. Switch to more efficient data structures.
3. Get reduced computational complexity.
#Challenge #4
A Convenient Hierarchy of Languages

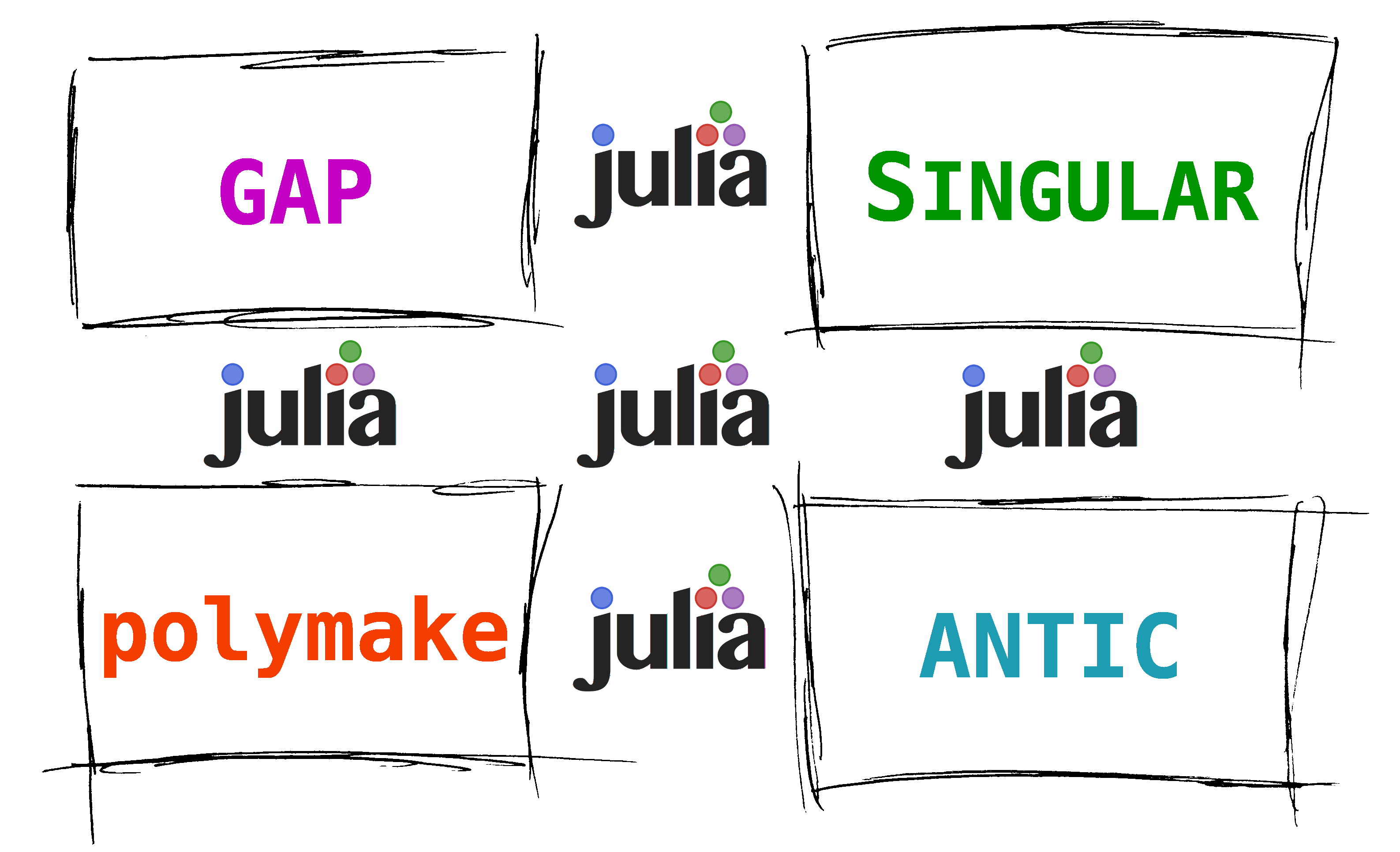
Who
What is  ?
> high-level dynamic programming
> language, also functional
> interactive shell: read-eval-print loop (REPL)
> just-in-time compilation
> good performance
> can call Python & C functions
> built-in package manager
> designed for parallel &
> distributed computing
#How will SINGULAR use Julia?
.
?
> high-level dynamic programming
> language, also functional
> interactive shell: read-eval-print loop (REPL)
> just-in-time compilation
> good performance
> can call Python & C functions
> built-in package manager
> designed for parallel &
> distributed computing
#How will SINGULAR use Julia?
.
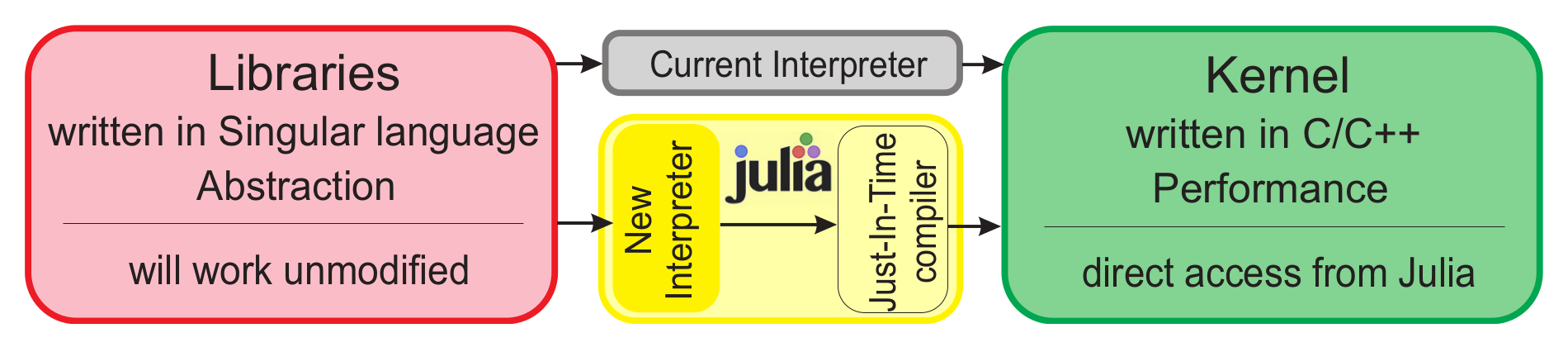 Still *experimental*
https://github.com/wbhart/Singular.jl
.
julia
julia> f(x) = 2x+1; g(x,y) = y+2f(x)
julia> println("I think", g(1,1), "is prime.")
I think 7 is prime.
.
julia> using Singular
#Challenge #5
Data Bases
Collect results of extensive
& time-consuming calculations
in *databases*.
Oh, and don't forget to make
them *publicly* available.
#Well, backups would
#be great, too
.
Bonjour,
nous venons malheureusement de perdre 2 disques
de données sur 10, simultanément, sur la machine xxx,
qui était en RAID 5.
A priori cela implique que *toutes les données sont perdues*.
#Challenge #6
Development Model
A single
OSCAR
repository
Conerstones are *submodules*
.
⇒ OSCAR references only a
single commit of a submodule
Development
Phase 1
(first 1/2 year)
0. Repository is private (oh no!)
1. All can push to OSCAR repository
2. CI only for compile success testing
3. Minimal tests
4. Set feature flags for broken parts
Development
Phase 2
0. Make repository public :)
1. Collaboration for everybody only
1. via tested pull requests
2. CI tests via Jenkins
3. Code review in pull requests
4. One main development branch,
4. branches for releases
#Challenge #7
Easy Access
#OpenDreamKit
Horizon 2020 European Research
Infrastructure project
.
Aim: Provide intuitive user interfaces.
Possible
Solution?
Give non-experts
*buttons*
to click on.
Still *experimental*
https://github.com/wbhart/Singular.jl
.
julia
julia> f(x) = 2x+1; g(x,y) = y+2f(x)
julia> println("I think", g(1,1), "is prime.")
I think 7 is prime.
.
julia> using Singular
#Challenge #5
Data Bases
Collect results of extensive
& time-consuming calculations
in *databases*.
Oh, and don't forget to make
them *publicly* available.
#Well, backups would
#be great, too
.
Bonjour,
nous venons malheureusement de perdre 2 disques
de données sur 10, simultanément, sur la machine xxx,
qui était en RAID 5.
A priori cela implique que *toutes les données sont perdues*.
#Challenge #6
Development Model
A single
OSCAR
repository
Conerstones are *submodules*
.
⇒ OSCAR references only a
single commit of a submodule
Development
Phase 1
(first 1/2 year)
0. Repository is private (oh no!)
1. All can push to OSCAR repository
2. CI only for compile success testing
3. Minimal tests
4. Set feature flags for broken parts
Development
Phase 2
0. Make repository public :)
1. Collaboration for everybody only
1. via tested pull requests
2. CI tests via Jenkins
3. Code review in pull requests
4. One main development branch,
4. branches for releases
#Challenge #7
Easy Access
#OpenDreamKit
Horizon 2020 European Research
Infrastructure project
.
Aim: Provide intuitive user interfaces.
Possible
Solution?
Give non-experts
*buttons*
to click on.
 #Credits
Mohamed Barakat, Janko Böhm,
Wolfram Decker, Claus Fieker,
Sebastian Gutsche, Gert-Martin Greuel,
Bill Hart, Tommy Hofmann,
Gunter Malle, Gerhard Pfister,
Lukas Ristau, Mathias Schulze,
Andreas Steenpaß, Isabel Stenger
& many more
One Last
Commercial Break
#ISSAC 2017
The 42nd International Symposium
on Symbolic and Algebraic Computation
University of Kaiserslautern, Gemany,
*July 25 - 28, 2017*
#PASCO 2017
International Workshop on Parallel
Symbolic Computation
University of Kaiserslautern, Gemany,
*July 23 - 24, 2017*
Thank you
for your
attention
Questions?
Remarks?
#Credits
Mohamed Barakat, Janko Böhm,
Wolfram Decker, Claus Fieker,
Sebastian Gutsche, Gert-Martin Greuel,
Bill Hart, Tommy Hofmann,
Gunter Malle, Gerhard Pfister,
Lukas Ristau, Mathias Schulze,
Andreas Steenpaß, Isabel Stenger
& many more
One Last
Commercial Break
#ISSAC 2017
The 42nd International Symposium
on Symbolic and Algebraic Computation
University of Kaiserslautern, Gemany,
*July 25 - 28, 2017*
#PASCO 2017
International Workshop on Parallel
Symbolic Computation
University of Kaiserslautern, Gemany,
*July 23 - 24, 2017*
Thank you
for your
attention
Questions?
Remarks?
 #polymake
convex polytopes, polyhedral fans,
simplicial complexes, related objects
from combinatorics & geometry
*polymake* - Normal fans (via SINGULAR)
.
> LIB"polymake.so"; // credits for polymake
> ring r=0,(x,y),dp;
> poly f=x3+y3+1; // last SINGULAR-only statement
.
> polytope p = newtonPolytope(f);
> fan F = normalFan(p);
> F;
RAYS: MAXIMAL CONES:
-1 -1 #0 {0 1} #Dimension 2
0 1 #1 {0 2}
1 0 #2 {1 2}
#polymake
convex polytopes, polyhedral fans,
simplicial complexes, related objects
from combinatorics & geometry
*polymake* - Normal fans (via SINGULAR)
.
> LIB"polymake.so"; // credits for polymake
> ring r=0,(x,y),dp;
> poly f=x3+y3+1; // last SINGULAR-only statement
.
> polytope p = newtonPolytope(f);
> fan F = normalFan(p);
> F;
RAYS: MAXIMAL CONES:
-1 -1 #0 {0 1} #Dimension 2
0 1 #1 {0 2}
1 0 #2 {1 2}
 #ANTIC
number theory software, computations
in & with number fields and generic
finitely presented rings
.
created within SPP-1489
*ANTIC* - Class Groups & Extended GCDs
.
> Qx, x = PolynomialRing(QQ, "x")
> f = x^6+141*x^5-141*x^4+141*x^3-141*x^2+141*x-141
> K, a = NumberField(f);
> M = lll(maximal_order(K));
> class_group(M)
.
> Kt, t = PolynomialRing(K, "t")
> g = sum([K(rand(M, 100))*t^i for i=1:20])
> h = sum([K(rand(M, 100))*t^i for i=1:20])
> @time gc, a, b = gcdx(g, h);
#ANTIC
number theory software, computations
in & with number fields and generic
finitely presented rings
.
created within SPP-1489
*ANTIC* - Class Groups & Extended GCDs
.
> Qx, x = PolynomialRing(QQ, "x")
> f = x^6+141*x^5-141*x^4+141*x^3-141*x^2+141*x-141
> K, a = NumberField(f);
> M = lll(maximal_order(K));
> class_group(M)
.
> Kt, t = PolynomialRing(K, "t")
> g = sum([K(rand(M, 100))*t^i for i=1:20])
> h = sum([K(rand(M, 100))*t^i for i=1:20])
> @time gc, a, b = gcdx(g, h);

 Design & development
of a CAS in general
driven by intended
applications
Mathematical
applications
Mumford (1980):
.
Can a computer classify all surfaces of
general type with pg = 0?
Let X be a minimal surface
of general type with pg=0
such that (KX)2 = 1
.
→ numerical *Godeaux surfaces*
X Godeaux surface
.
⇒ H1(X,ℤ) is cyclic of
⇒ order at most 5
.
Constructions have been
given for each such order.
Conjecture:
.
There is precisely one irreducible
family of surfaces for each order.
Experimental approach to
solve this conjecture:
.
1. Construct random points
1. in moduli spaces.
.
2. Study related geometry
2. via CAS.
Requirements for this approach:
.
1. Computational Algebraic Geometry
2. Topology
3. Group Theory
Joint project by
.
Wolfram Decker & Isabel Stenger
(Kaiserslautern)
Frank-Olaf Schreyer
(Saarbrücken)
.
in collaboration with Miles Reid
(Warwick)
Why is this computationally hard
from the very beginning?
.
> Rextension;
// characteristic : 0
// 1 parameter : a
// minpoly :
(24873879473832817299558394474990433025260537858429700*a^8
+412197480758832021377448558823165698794277118212212070*a^7
+625366891611244986389942014312773193649951168354090190*a^6
-436561073546512334083477547357856090524552855592558795*a^5
-914947642504230095779800456657440020138074539186145912*a^4
-2227325279423247966617649640155997715235288113299887954*a^3
+2312070077580715288467637707530192772778088469836344950*a^2
+1366053134215201364075122803745127996518986576734818612*a
-1156759915557562158859054495379551857229358735237021536)
// number of vars : 12
"Non-mathematical"
applications
#High Energy Phsyics
joint work with
Pierpaolo Mastrolia and Tiziano Peraro
Design & development
of a CAS in general
driven by intended
applications
Mathematical
applications
Mumford (1980):
.
Can a computer classify all surfaces of
general type with pg = 0?
Let X be a minimal surface
of general type with pg=0
such that (KX)2 = 1
.
→ numerical *Godeaux surfaces*
X Godeaux surface
.
⇒ H1(X,ℤ) is cyclic of
⇒ order at most 5
.
Constructions have been
given for each such order.
Conjecture:
.
There is precisely one irreducible
family of surfaces for each order.
Experimental approach to
solve this conjecture:
.
1. Construct random points
1. in moduli spaces.
.
2. Study related geometry
2. via CAS.
Requirements for this approach:
.
1. Computational Algebraic Geometry
2. Topology
3. Group Theory
Joint project by
.
Wolfram Decker & Isabel Stenger
(Kaiserslautern)
Frank-Olaf Schreyer
(Saarbrücken)
.
in collaboration with Miles Reid
(Warwick)
Why is this computationally hard
from the very beginning?
.
> Rextension;
// characteristic : 0
// 1 parameter : a
// minpoly :
(24873879473832817299558394474990433025260537858429700*a^8
+412197480758832021377448558823165698794277118212212070*a^7
+625366891611244986389942014312773193649951168354090190*a^6
-436561073546512334083477547357856090524552855592558795*a^5
-914947642504230095779800456657440020138074539186145912*a^4
-2227325279423247966617649640155997715235288113299887954*a^3
+2312070077580715288467637707530192772778088469836344950*a^2
+1366053134215201364075122803745127996518986576734818612*a
-1156759915557562158859054495379551857229358735237021536)
// number of vars : 12
"Non-mathematical"
applications
#High Energy Phsyics
joint work with
Pierpaolo Mastrolia and Tiziano Peraro

 For example,
.
> ring r=(0,p11,p12,p22,e34,m1,m2,m3),(x1,x2,x3,x4),dp;
.
> poly D1=2*x3*x4*e34+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-m1;
> poly D2=-m2+2*x3*x4*e34-2*p11*x1+p11+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-2*p12*x2;
> poly D3=2*x3*x4*e34+2*x1*p12-m3+x1*(p11*x1+p12*x2)+p22
. +(x1*p12+p22*x2)*x2+2*p22*x2;
.
> ideal I = D1, D2, D3;
> ideal GI = groebner(I);
#Challenge #1
Efficiency of Fundamental Algorithms
Low level Implementations
.
*Gröbner Bases* & *Standard Bases*
*Syzygies* & *Free Resolutions*
*Polynomial Factorization*
*F4 Algorithm* for SINGULAR
.
based on special-purpose
linear algebra library *GBLA*
.
joint work with
Jean-Charles Faugère
& the PolSys team
For example,
.
> ring r=(0,p11,p12,p22,e34,m1,m2,m3),(x1,x2,x3,x4),dp;
.
> poly D1=2*x3*x4*e34+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-m1;
> poly D2=-m2+2*x3*x4*e34-2*p11*x1+p11+x1*(p11*x1+p12*x2)
. +(x1*p12+p22*x2)*x2-2*p12*x2;
> poly D3=2*x3*x4*e34+2*x1*p12-m3+x1*(p11*x1+p12*x2)+p22
. +(x1*p12+p22*x2)*x2+2*p22*x2;
.
> ideal I = D1, D2, D3;
> ideal GI = groebner(I);
#Challenge #1
Efficiency of Fundamental Algorithms
Low level Implementations
.
*Gröbner Bases* & *Standard Bases*
*Syzygies* & *Free Resolutions*
*Polynomial Factorization*
*F4 Algorithm* for SINGULAR
.
based on special-purpose
linear algebra library *GBLA*
.
joint work with
Jean-Charles Faugère
& the PolSys team





 High level Implementations
*Primary decomposition*
(Gianni-Trager-Zacharias,
Shimoyama-Yokoyama,
Eisenbud-Huneke-Vasconcelos)
.
*Normalization*
(de Jong, Greuel-Laplagne-Seelisch)
.
analyzing *Singularities*
(Hamburger-Noether expansions, blow-ups,
resolution of singularities, etc.)
Other Packages
High level Implementations
*Primary decomposition*
(Gianni-Trager-Zacharias,
Shimoyama-Yokoyama,
Eisenbud-Huneke-Vasconcelos)
.
*Normalization*
(de Jong, Greuel-Laplagne-Seelisch)
.
analyzing *Singularities*
(Hamburger-Noether expansions, blow-ups,
resolution of singularities, etc.)
Other Packages
 *CHEVIE*
Symbolic calculations with generic
character tables of groups
of Lie type & more
(Geck-Hiß-Lübeck-Malle-Michel-Pfeiffer)
*homalg*
Constructive homological algebra
(Barakat-Gutsche-Lange-Hegemann-Posur)
.
*CAP*
Category theory part for homalg
(Gutsche-Posur)
*FLINT*
Fast library for number theory
(Hart-Johansson-et al)
*NEMO*
Algebraic number theory,
recursive generic rings
(Fieker-Hart-Hofmann-Johansson-Motsak)
*HECKE*
Class groups, orders in number fields,
lattice enumeration, sparse linear algebra
(Fieker-Hofmann)
*A-TINT*
Algorithmic tropical
intersection theory
(Hampe)
even more packages
.
*4ti2*
*cddlib*
*Gfan*
*normaliz*
& many more
Challenge #2
Parallelization
Thread Level
(fine grain)
*CHEVIE*
Symbolic calculations with generic
character tables of groups
of Lie type & more
(Geck-Hiß-Lübeck-Malle-Michel-Pfeiffer)
*homalg*
Constructive homological algebra
(Barakat-Gutsche-Lange-Hegemann-Posur)
.
*CAP*
Category theory part for homalg
(Gutsche-Posur)
*FLINT*
Fast library for number theory
(Hart-Johansson-et al)
*NEMO*
Algebraic number theory,
recursive generic rings
(Fieker-Hart-Hofmann-Johansson-Motsak)
*HECKE*
Class groups, orders in number fields,
lattice enumeration, sparse linear algebra
(Fieker-Hofmann)
*A-TINT*
Algorithmic tropical
intersection theory
(Hampe)
even more packages
.
*4ti2*
*cddlib*
*Gfan*
*normaliz*
& many more
Challenge #2
Parallelization
Thread Level
(fine grain)


 *Problem*
Many fundamental algorithms
are sequential in nature
Process Level
(coarse grain)
General scheme for
*modular methods*
for algorithms
over the rationals.
e.g. GBs over the rationals
(Arnold, Idrees-Pfister-Steidel,
(& many more)
or GBs over algebraic number fields
(Boku-Decker-Fieker-Steenpaß)
*Problem*
Many fundamental algorithms
are sequential in nature
Process Level
(coarse grain)
General scheme for
*modular methods*
for algorithms
over the rationals.
e.g. GBs over the rationals
(Arnold, Idrees-Pfister-Steidel,
(& many more)
or GBs over algebraic number fields
(Boku-Decker-Fieker-Steenpaß)
 Or try to find new approaches
*Local-to-global Approach* to Normalization
(Böhm-Decker-Laplagne-Pfister-Steenpaß-Steidel)
.
1. Stratify the singular locus.
2. Compute local contribution to the
2. normalization at each stratum.
3. Put the local contributions back together.
How to combine different
levels of parallelization
in a *convenient* way?
.
Experts? Non-experts?
*Btw:*
x86 CPUs are not the
whole picture
Or try to find new approaches
*Local-to-global Approach* to Normalization
(Böhm-Decker-Laplagne-Pfister-Steenpaß-Steidel)
.
1. Stratify the singular locus.
2. Compute local contribution to the
2. normalization at each stratum.
3. Put the local contributions back together.
How to combine different
levels of parallelization
in a *convenient* way?
.
Experts? Non-experts?
*Btw:*
x86 CPUs are not the
whole picture
 #Cluster of 256 Raspberry Pis
(src: https://www.raspberrypi.org/magpi/seemore/)
massively-parallel multicore processors,
on-chip / discrete GPUs, ARM chips,
heterogenous computation (OpenCL),
distributed computation on our
phones & tablets, ...
#Challenge #3
Make Abstract Concepts of Pure
Mathematicians Constructive
*Category Theory*
influenced object-oriented
& functional programming
#Cluster of 256 Raspberry Pis
(src: https://www.raspberrypi.org/magpi/seemore/)
massively-parallel multicore processors,
on-chip / discrete GPUs, ARM chips,
heterogenous computation (OpenCL),
distributed computation on our
phones & tablets, ...
#Challenge #3
Make Abstract Concepts of Pure
Mathematicians Constructive
*Category Theory*
influenced object-oriented
& functional programming
 #Wormholes in mathematics
#Wormholes in mathematics
 (license: GNU-FDL, made by Panzi)
1. Translate problems in entirely different context.
2. Switch to more efficient data structures.
3. Get reduced computational complexity.
#Challenge #4
A Convenient Hierarchy of Languages
(license: GNU-FDL, made by Panzi)
1. Translate problems in entirely different context.
2. Switch to more efficient data structures.
3. Get reduced computational complexity.
#Challenge #4
A Convenient Hierarchy of Languages


 ?
> high-level dynamic programming
> language, also functional
> interactive shell: read-eval-print loop (REPL)
> just-in-time compilation
> good performance
> can call Python & C functions
> built-in package manager
> designed for parallel &
> distributed computing
#How will SINGULAR use Julia?
.
?
> high-level dynamic programming
> language, also functional
> interactive shell: read-eval-print loop (REPL)
> just-in-time compilation
> good performance
> can call Python & C functions
> built-in package manager
> designed for parallel &
> distributed computing
#How will SINGULAR use Julia?
.
 Still *experimental*
https://github.com/wbhart/Singular.jl
.
julia
julia> f(x) = 2x+1; g(x,y) = y+2f(x)
julia> println("I think", g(1,1), "is prime.")
I think 7 is prime.
.
julia> using Singular
#Challenge #5
Data Bases
Collect results of extensive
& time-consuming calculations
in *databases*.
Oh, and don't forget to make
them *publicly* available.
#Well, backups would
#be great, too
.
Bonjour,
nous venons malheureusement de perdre 2 disques
de données sur 10, simultanément, sur la machine xxx,
qui était en RAID 5.
A priori cela implique que *toutes les données sont perdues*.
#Challenge #6
Development Model
A single
OSCAR
repository
Conerstones are *submodules*
.
⇒ OSCAR references only a
single commit of a submodule
Development
Phase 1
(first 1/2 year)
0. Repository is private (oh no!)
1. All can push to OSCAR repository
2. CI only for compile success testing
3. Minimal tests
4. Set feature flags for broken parts
Development
Phase 2
0. Make repository public :)
1. Collaboration for everybody only
1. via tested pull requests
2. CI tests via Jenkins
3. Code review in pull requests
4. One main development branch,
4. branches for releases
#Challenge #7
Easy Access
#OpenDreamKit
Horizon 2020 European Research
Infrastructure project
.
Aim: Provide intuitive user interfaces.
Possible
Solution?
Give non-experts
*buttons*
to click on.
Still *experimental*
https://github.com/wbhart/Singular.jl
.
julia
julia> f(x) = 2x+1; g(x,y) = y+2f(x)
julia> println("I think", g(1,1), "is prime.")
I think 7 is prime.
.
julia> using Singular
#Challenge #5
Data Bases
Collect results of extensive
& time-consuming calculations
in *databases*.
Oh, and don't forget to make
them *publicly* available.
#Well, backups would
#be great, too
.
Bonjour,
nous venons malheureusement de perdre 2 disques
de données sur 10, simultanément, sur la machine xxx,
qui était en RAID 5.
A priori cela implique que *toutes les données sont perdues*.
#Challenge #6
Development Model
A single
OSCAR
repository
Conerstones are *submodules*
.
⇒ OSCAR references only a
single commit of a submodule
Development
Phase 1
(first 1/2 year)
0. Repository is private (oh no!)
1. All can push to OSCAR repository
2. CI only for compile success testing
3. Minimal tests
4. Set feature flags for broken parts
Development
Phase 2
0. Make repository public :)
1. Collaboration for everybody only
1. via tested pull requests
2. CI tests via Jenkins
3. Code review in pull requests
4. One main development branch,
4. branches for releases
#Challenge #7
Easy Access
#OpenDreamKit
Horizon 2020 European Research
Infrastructure project
.
Aim: Provide intuitive user interfaces.
Possible
Solution?
Give non-experts
*buttons*
to click on.

 #Credits
Mohamed Barakat, Janko Böhm,
Wolfram Decker, Claus Fieker,
Sebastian Gutsche, Gert-Martin Greuel,
Bill Hart, Tommy Hofmann,
Gunter Malle, Gerhard Pfister,
Lukas Ristau, Mathias Schulze,
Andreas Steenpaß, Isabel Stenger
& many more
One Last
Commercial Break
#ISSAC 2017
The 42nd International Symposium
on Symbolic and Algebraic Computation
University of Kaiserslautern, Gemany,
*July 25 - 28, 2017*
#PASCO 2017
International Workshop on Parallel
Symbolic Computation
University of Kaiserslautern, Gemany,
*July 23 - 24, 2017*
Thank you
for your
attention
Questions?
Remarks?
#Credits
Mohamed Barakat, Janko Böhm,
Wolfram Decker, Claus Fieker,
Sebastian Gutsche, Gert-Martin Greuel,
Bill Hart, Tommy Hofmann,
Gunter Malle, Gerhard Pfister,
Lukas Ristau, Mathias Schulze,
Andreas Steenpaß, Isabel Stenger
& many more
One Last
Commercial Break
#ISSAC 2017
The 42nd International Symposium
on Symbolic and Algebraic Computation
University of Kaiserslautern, Gemany,
*July 25 - 28, 2017*
#PASCO 2017
International Workshop on Parallel
Symbolic Computation
University of Kaiserslautern, Gemany,
*July 23 - 24, 2017*
Thank you
for your
attention
Questions?
Remarks?